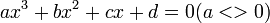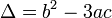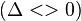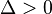Tổng Tổng hợp các dạng giải phương trình bậc 3 và bất phương trình bật 3 giúp cho các em ôn thi tốt môn giải phương trình do trung tam day kem tai nha tphcm chia sẽ.
Cách giải phương trình bậc 3 bằng phương pháp Cardano
Trước tiên, chia phương trình cho α3 để đưa về dạng
Đặt x = t – a/3 và biến đổi ta có phương trình
trong đó
và
Nó được gọi là phương trình bậc ba suy biến.
Ta sẽ tìm các số u và v sao cho
và
một nghiệm của nó tìm được từ việc đặt
có thể kiểm tra trực tiếp khi thay giá trị t vào (2), nhờ hằng đảng thức lập phương của nhị thức
Hệ (3) có thể giải từ phương trình thứ hai rút v, ta có
Thay vào phương trình thứ nhất trong (3) ta có
Phương trình này tương đương với một phương trình bậc hai với u3. Khi giải, ta tìm được (chứa căn bậc 3)
Vì t = v − u và t = x + a/3, ta tìm được
Phương pháp lượng giác và tổng hợp
Đây là phần tóm tắt kết quả bài giải phương trình bậc ba:
Đặt các giá trị:
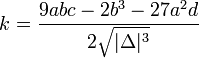
1) Nếu
- 1.1) |k| ≤ 1: Phương trình có ba nghiệm
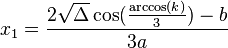
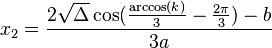
- 1.2) |k| > 1: Phương trình có một nghiệm duy nhất
![x = \frac{\sqrt{\Delta}|k|}{3ak}\left(\sqrt[3]{|k|+\sqrt{k^2-1}}+\sqrt[3]{|k|-\sqrt{k^2-1}}\right)-\frac{b}{3a}](https://upload.wikimedia.org/math/7/f/6/7f603b3dae7d0a89de68acfeb6eec5ee.png)
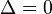 : Phương trình có một nghiệm bội
: Phương trình có một nghiệm bội
![x = \frac{-b+\sqrt[3]{b^3-27a^2d}}{3a}](https://upload.wikimedia.org/math/9/d/3/9d388b6b6738db93c5d0c355d5996cb4.png)
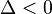 : Phương trình có một nghiệm duy nhất
: Phương trình có một nghiệm duy nhất
![x = \frac{\sqrt{|\Delta|}}{3a}\left(\sqrt[3]{k+\sqrt{k^2+1}}+\sqrt[3]{k-\sqrt{k^2+1}}\right)-\frac{b}{3a}](https://upload.wikimedia.org/math/1/1/a/11aa47361d83e22299ab8d9f14b4b4c7.png)

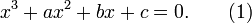
 trong đó
trong đó  và
và 
 và
và 


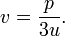

![u=\sqrt[3]{{q\over 2}\pm \sqrt{{q^{2}\over 4}+{p^{3}\over 27}}}. \qquad (4)](https://upload.wikimedia.org/math/4/4/c/44ce6b82d14c0b84e05b23c6db35b166.png)